By: Dr. Nayana Das, Research Engineer, LTIMindtree

In our previous blog, Quantum Computers: The Looming Threat to Current Digital Security, we discussed the imminent threat that quantum computers pose to existing cryptographic systems. Their advanced algorithms could potentially dismantle today’s encryption standards, creating a pressuring need for more robust security methods. While Quantum Key Distribution (QKD) offers secure communication channels using the principles of quantum mechanics, it struggles with scalability due to infrastructure and distance constraints.

This is where Post-Quantum Cryptography (PQC) comes in, offering a more practical and scalable solution by creating quantum-resistant algorithms that can be integrated into existing systems with minimal disruption. This makes PQC an essential defense against the quantum threat. With advancements in quantum-resistant cryptography, we’re not just preparing for the future, we’re actively defending it today.

In this blog, let’s delve deeper into lattice-based cryptography, one of the most promising PQC techniques. This cryptography forms the foundation of two of the three National Institute of Standards and Technology (NIST)-standardized algorithms, providing quantum-resistant security for communication in the quantum age.

NIST’s Standardization of Post-Quantum Algorithms

The NIST has taken charge of evaluating and standardizing quantum-resistant cryptographic algorithms. ^I Their goal? To ensure our encryption systems are prepared to withstand the power of quantum computing. But what does this mean for general encryption and digital signatures—the two pillars of cryptographic security?

NIST recently finalized four algorithms tailored to these tasks:

1. CRYSTALS-Kyber for general encryption
2. CRYSTALS-Dilithium, SPHINCS+, and FALCON for digital signatures

Earlier drafts of three standards have already been released, with the fourth standard, based on FALCON, anticipated to follow soon.

Although the final versions of the standards have not changed significantly from the draft versions, NIST renamed the algorithms to better reflect the specific encryption methods or signature types used in the finalized standards. These new standards were officially published on August 13, 2024 ⁱⁱ  under the following Federal Information Processing Standards (FIPS):

FIPS 203

It is based on CRYSTALS-Kyber, now renamed ML-KEM (Module-Lattice-based Key-Encapsulation Mechanism). ⁱⁱⁱ This standard focuses on general encryption, providing efficient key exchanges for secure public communication.

FIPS 204

It is based on CRYSTALS-Dilithium, now called ML-DSA (Module-Lattice-Based Digital Signature Algorithm).^iv This standard specializes in fast, secure digital signatures for identity verification and data integrity.

FIPS 205

It is based on SPHINCS+, now named SLH-DSA (Stateless Hash-Based Digital Signature Algorithm).^v It offers hash-based digital signatures, serving as a backup to ML-DSA for enhanced long-term security.

Together, these algorithms represent a giant leap forward in post-quantum cryptography, addressing both current and future security needs.

The Role of Lattice-based Cryptography in Post-Quantum Security

Lattice-based cryptography is a cornerstone of PQC.^vi But what exactly is a lattice, and why does it matter?

What is a Lattice?

Think of a lattice as a multi-dimensional grid of points arranged in a structured pattern. If you were dropped into a forest of trees stretching infinitely in every direction, how would you find a single, specific tree? Now imagine this forest exists in hundreds of dimensions. That’s the level of complexity quantum computers face when attempting to break lattice-based encryption.

Fig 1: Lattice Structure

Source: http://www.graylark.com/eve/lattices.html

This complexity makes lattices the perfect foundation for quantum-resistant cryptography. Algorithms like CRYSTALS-Kyber and CRYSTALS-Dilithium are built on two hard-to-solve mathematical problems:

Shortest Vector Problem (SVP)

The Shortest Vector Problem (SVP) revolves around finding the shortest non-zero-line segment, or vector, between points in a lattice—a grid-like structure created using basis vectors. While it’s easy to generate points by scaling and combining these vectors, identifying the shortest vector is far more complex.

For example, even in a two-dimensional lattice, determining the shortest path requires testing several combinations. As dimensions increase, the challenge grows exponentially with the vast number of possible vectors to explore.

Public keys in SVP are created using two types of bases:

• Good Basis: Vectors are near-perpendicular, making calculations easier.
• Bad Basis: Vectors are nearly parallel, making the problem more complex.

The private key is the good basis, allowing the receiver to decode messages efficiently, while the public key is the bad basis, used by the sender to encrypt data. This unique structure underpins the strength of quantum-resistant cryptography.

Learning With Errors (LWE)

The Learning with Errors (LWE) problem adds random noise to simple equations, making it tough to reverse-engineer the original values. Here’s how it works:

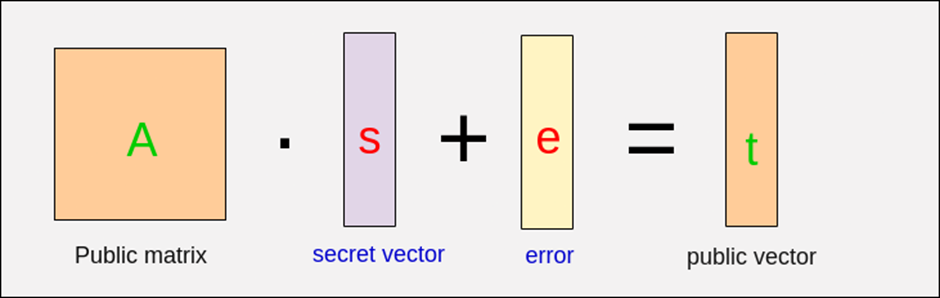
Fig 2: Simple LWE Model

Source: https://medium.com/@aditya.koranga/learning-with-errors-quantum-proof-algorithm-f43a6599fca7

Given a secret vector ‘s’, a public matrix ‘A’, and a small noise vector ‘e’, the output is generated as b = As + e mod q, where ‘q’ is a modulus. Here, ‘b’ hides the secret ‘s’ by adding random noise ‘e’, making it challenging to reverse the process.

While the equation seems straightforward, the noise introduces ambiguity, making it computationally hard to retrieve the secret vector ‘s’, even with powerful quantum computers.

In LWE-based cryptography, the pair (A,b) (A, b) (A,b) forms the public key, while ‘s’ remains the private key. The noise ensures that even if a quantum computer attempts to decode the data, it faces significant complexity. These two problems provide the foundation for secure encryption and digital signatures in lattice-based cryptography.

Why Lattice-based Cryptography Matters?

Lattice-based cryptography is a key technique in quantum-resistant cryptography and plays a critical role in the fight against quantum attacks for several reasons:

1. Quantum Resistance: It is built on problems like SVP and LWE that are computationally hard for quantum computers to solve. This makes it extremely secure against potential quantum threats.
2. Versatility: Lattice-based methods can be used for both encryption and digital signatures, making them suitable for various security applications.
3. Efficiency: The algorithms like CRYSTALS-Kyber and CRYSTALS-Dilithium are efficient, scalable, and practical for real-world applications without heavy computational burden.

Conclusion: Securing the Future with Lattice-based Cryptography

With the quantum era on the horizon, traditional encryption methods will fall short. Lattice-based cryptography offers a robust and reliable solution, ensuring secure communications and data protection against emerging quantum threats.

By adopting standardized algorithms like CRYSTALS-Kyber and CRYSTALS-Dilithium, we can pave the way for a future built on quantum-resistant security.

Stay tuned for our next blog, where we’ll delve into hash-based cryptography, another critical pillar of quantum-resistant cryptography, and its role in safeguarding the digital world.

Both the methods must be expanded to state the forward and reverse problems. Give an intuition on the complexity of the reverse problem. Also state how the public key is generated.

References

ⁱ Post-Quantum Cryptography PQC, NIST: https://csrc.nist.gov/projects/post-quantum-cryptography

ⁱⁱ NIST Releases First 3 Finalized Post-Quantum Encryption Standards, NIST: https://www.nist.gov/news-events/news/2024/08/nist-releases-first-3-finalized-post-quantum-encryption-standards

ⁱⁱⁱ Module-Lattice-Based Key-Encapsulation Mechanism Standard, NIST: https://csrc.nist.gov/pubs/fips/203/final

^iv Module-Lattice-Based Digital Signature Standard, NIST: https://csrc.nist.gov/pubs/fips/204/final

^v Stateless Hash-Based Digital Signature Standard, NIST:  https://csrc.nist.gov/pubs/fips/205/final

^vi Lattice-based Cryptography, Sringer Nature: https://link.springer.com/chapter/10.1007/978-3-540-88702-7_5